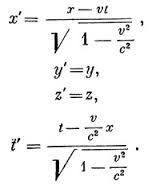Развитие квантовой химии в СССР началось в 1931 году, когда в физико-химическом институте им. Л.Я. Карпова профессор Я.К. Сыркин основал лабораторию строения вещества и спектроскопии. В 1934 году по рекомендации Ю.Б. Румера в Москву пригласили работать молодого немецкого учёного-антифашиста Ганса Гельмана. В 1937 г. увидела свет его монография «Квантовая химия» (её немецкое издание вышло в Вене незадолго до аншлюса), ставшая основным учебником для нескольких поколений советских исследователей в этой области. Известна фундаментальная теорема Гельмана—Фейнмана (Ричард Фейнман сформулировал её независимо).

Однако жизнь этого талантливого человека, ставшего в июне 1936 г. советским гражданином, вскоре оборвалась: в марте 1938 г. он был арестован, обвинён в шпионаже и расстрелян. Ему было 34 года.

Наш старейший квантовый химик и спектроскопист д.ф.-м.наук, проф. Михаил Аркадьевич Ковнер (1910—2006) хорошо знал Гельмана: он был одним из переводчиков его книги; именно Ганс Гельман дал Ковнеру тему для кандидатской диссертации (исследование вопроса о природе связи в молекуле аммиака), став его научным руководителем. Ковнер успешно защитился в конце 1938 года, когда Гельмана уже не было в живых.

Михаил Аркадьевич считал себя учеником Гельмана и прикладывал большие усилия, чтобы сделать его имя известным новым поколениям физикохимиков. Будучи уже в преклонном возрасте, но продолжая работать в Институте истории естествознания и техники РАН, он написал статью «Ганс Гельман и рождение квантовой химии», опубликованную в ХиЖ (2000, № 5; я был редактором): < Гельман_Ковнер> (или <Гельман>).

А вскоре после этого в серии  «Научно-биографическая литература» вышла небольшая книга М.А. Ковнера «Ганс Густавович Гельман» (М.: Наука, 2002), в которой Михаил Аркадьевич подробно рассказал о жизни и трудах своего учителя.

В 1966 г. вышла брошюра — сборник статей известных физиков на тему «Теория относительности и физика высоких энергий» (М.: Знание). Профессор Евгений Львович Фейнберг (1912—2005; академик с 1997 г.) в своей статье писал:

«Давно прошло то время, когда некомпетентные недоброжелатели старались опровергнуть теорию относительности, — невероятную, страшную, противоречащую здравому смыслу. Давно прошло и то время, когда некомпетентные доброжелатели пытались пригладить теорию относительности, сделав её менее странной, например, старались убедить, что сокращение тела есть только кажущийся эффект, что время только кажущимся образом замедляется, что формулы теории относительности дают только рецепт вычисления физических величин, но не меняют ничего в понимании пространства и времени и т.д. Всё это ушло в прошлое, и сейчас теория относительности для более молодых поколений кажется совершенно естественной и такой же классической, привычной теорией, как классическая механика Ньютона или электродинамика».

Я в год выхода брошюры как раз закончил школу, то есть был представителем «молодого поколения», о котором сказал Фейнберг. И в старших классах уже пытался — по научно-популярным книгам, которых было много, — разобраться в этой теории, но совершенно ничего не мог в ней понять (больше всего времени я уделил книге Ю.И.Соколовского «Теория относительности в элементарном изложении»).

Отсюда можно было сделать два вывода: 1) что я не гожусь в физики; 2) что с теорией не всё в порядке. Я сделал второй и стал то ли некомпетентным недоброжелателем, то ли некомпетентным доброжелателем ТО. А ровно через двадцать лет понял, в чём там ошибка.

В 1997 вышла книга «Пристрастие» (М.: Аграф) нашего замечательного учёного, мыслителя Бориса Викторовича Раушенбаха (1915—2001). Это сборник его статей на разные нематематические темы, опубликованных в разные годы.

Я написал маленькую рецензию на неё, напечатанную в ХиЖ (1998, № 3). Привожу её:

Знаменитый дирижер Бруно Вальтер сказал: «Только музыкант — это всего лишь полумузыкант». Наверное, то же самое и с той же долей преувеличения верно и для физиков, химиков, инженеров. Да, наш век не был благоприятен для всестороннего развития личности, он шел под знаком специализации. И все же есть счастливые исключения, в которые попадает известный ученый в области ракетостроения и космонавтики академик Борис Викторович Раушенбах. В этой книге собраны ранее опубликованные его статьи на темы, не связанные непосредственно с профессиональной деятельностью академика, а таких оказалось очень много: живопись и психология творчества, история науки и религии, будущее нашей страны и всей цивилизации.

Когда-то он столкнулся с важной для космонавтики проблемой: как лучше изображать на экране пространственные объекты — то, над чем всегда бились художники. Она побудила его познакомиться с методами, которыми они пользовались. Так на его месте, вероятно, поступили бы и другие. Но Раушенбах не просто ознакомился, но глубоко изучил всю многовековую историю живописи, выработал общую точку зрения и написал уже несколько книг по теории перспективы в живописи и иконописи, да таких, что из них много нового для себя узнают искусствоведы.

Как отмечает сам автор, логическое мышление и естественнонаучный стиль у него превалируют и в гуманитарных сферах. Он доводит мысль до логического конца, каким бы парадоксальным тот, на первый взгляд, ни казался. Так, богословы вряд ли согласятся с его математической моделью Троицы в виде вектора трехмерного пространства и его ортогональных составляющих. Однако, как убедительно доказывает Раушенбах, с логической точки зрения модель работает хорошо.

Читать далее

Выдающийся советский физик академик Леонид Исаакович Мандельштам (1879—1944) в 1925 г. возглавил кафедру теоретической физики в МГУ. Его лекции и семинары охватывали широкий круг тем, и многие слушатели отмечали глубину и ясность его изложения. В 1972 г. была издана книга «Лекции по оптике, теории относительности и квантовой механике» (М.: Наука), куда вошли и его лекции по физическим основам теории относительности (1933—1934 гг.).

Отметим две вещи. Первое: лектор стремился при рассмотрении всякой проблемы предварительно прояснить её «на пальцах» и только после этого переходил к формализации. Второе: в те годы ТО ещё не закостенела, различные её аспекты живо дискутировались.

В десятой лекции Мандельштам говорит о преобразованиях Лоренца и следствиях из них. Приведу фрагмент (стр. 208; буквенные обозначения изменены):

Я хотел бы обратить внимание на одно обстоятельство. Мы искали преобразование так, чтобы из X² + Y² + Z² – C²T² = О 

следовало X`<sup>2</sup> + Y`² + Z`<sup>2</sup> – C<sup>2</sup>T`² = О.

Но мы вовсе не требовали, чтобы в том случае,

когда X² + Y² + Z² – C²T² = M 

при подстановке вместо X, Y, Z, T координат  X`, Y`, Z`, T` 

это выражение сохраняло то же самое значение.

Мы полагали X`<sup>2</sup> + Y`² + Z`<sup>2</sup> – C<sup>2</sup>T`² = K²(X² + Y² + Z² – C²T² ),

но оказалось, что  K² = 1.

Таким образом, если X² + Y² + Z² – C²T² = M, то при подстановке X`, Y`, Z`, T` вместо X, Y, Z, T мы получим опять 

X`<sup>2</sup> + Y`² + Z`<sup>2</sup> – C<sup>2</sup>T`² = M, то есть эта квадратичная форма инварианта по отношению к лоренцовому преобразованию.

Это больше, чем мы требовали.

===============================================================

«Это больше, чем мы требовали». Да, тут-то и кроется ошибка.

Время от времени у нас выходят книги японских учёных. Из тех, что я читал, вспомню «Лекции по физике» знаменитого Хидеки Юкавы (М.: Энергоиздат, 1981), «Кварки» Ёитиро Намбу (М.: Мир, 1984) и «К чему пришла физика» Рёю Утиямы (М.: Знание, 1986). Остановлюсь на последней — это маленькая книжка известного физика-теоретика, в которой на доступном уровне обсуждаются некоторые тонкие вещи, например понятие калибровочного поля (в его развитии автор принял активное участие).

Лично для меня книга Утиямы (1916—1990) оказалась очень полезной (ранее, в 1979 г. у нас вышла его «Теория относительности»). Симпатична и личность автора, с редкой искренностью рассказавший о перипетиях своей научной карьеры. В предисловии акад. Виталий Лазаревич Гинзбург отметил, что «книга весьма нестандартна, необычна в ряде отношений. Последнее относится и к стилю изложения, как-то отражающему специфику далёкой от нас японской культуры… Тут и объявление Эйнштейна мессией, и пояснение, касающиеся планов вступления автора в брак. Наконец, последняя глава книжки под названием «Горькие сожаления» в значительной мере носит автобиографический характер«.

Да, японский менталитет имеет свои особенности, которые отражаются и на научной деятельности. Более подробно это осветил в статье «Воспитание химика: от сердца к сердцу» японский физикохимик профессор Козо Кучицу. Он писал: «Я хочу на своём личном примере проследить влияние наших национальных культурных традиций на становление химика». Мой сокращённый перевод из журнала «The Chemical Intelligencer» был напечатан в ХиЖ (2002, № 7) <Кучицу>.

Американский физик Шелдон Глэшоу, который в этом году отметит 85-летие, знаменит тем, что стал одним из создателей теории электрослабых взаимодействий, объединившей электромагнитные и слабые силы. За это достижение вместе с Абдусом Саламом и Стивеном Вайнбергом был удостоен Нобелевской премии в 1979 г. — даже раньше, чем предсказанные ими частицы-переносчики слабых сил (W и Z мезоны) были обнаружены экспериментально (это произошло несколькими годами позже в ЦЕРНе). Также Глэшоу развил теорию кварков — обосновал существование, в дополнение к тройке Гелл-Манна, четвёртого кварка, названного «очарованным».

Он родился в Нью-Йорке, а его родители были родом из Бобруйска. В 1958 г. Глэшоу, получив стипендию для продолжения образования в Европе, хотел пройти стажировку в Физическом институте АН СССР под руководством Игоря Евгеньевича Тамма. Однако и его усилия, и хлопотавших за него профессоров оказались напрасны: разрешения приехать в нашу страну он не получил (отказали в визе).

Нужно сказать, что взгляды Глэшоу на современную теоретическую физику нестандартны: он скептически и критически относится к популярной теории суперструн, так как она не делает проверяемых на опыте предсказаний. Данное направление иногда называют «опереточной физикой» или «занимательной математикой», и Глэшоу даже попытался искоренить его в родном Гарварде, но это ему не удалось; учёный признает, что в своём мнении обычно оказывается в явном меньшинстве: «Я чувствую себя динозавром в мире выскочек-млекопитающих».

В 2002 г. у нас вышел перевод его книги «Очарование физики» (М.: РХД). Её составили
статьи разных жанров — автобиографические, эссе о науке и учёных, научные — о проблемах теории элементарных частиц. Я написал большую рецензию на неё — «Физика частиц: от лоскутного одеяла к гобелену», опубликованную в ХиЖ (2003, № 12): <Глэшоу>.

Отмечу ещё, что в своей статье «Платоновы тела и элементарные частицы» (ХиЖ, 2006, № 6) я кое-что говорил о предложенной Глэшоу и Говардом Джорджи геометрической модели, наглядно представляющей одно поколение фундаментальных фермионов: <Платоновы> или <ПлатЭлЧаст>.

Встретил в Сети выпущенный в 1985 г. Препринт (Институт атомной энергии им. И.В. Курчатова)

АЛЕКСАНДРА ЛЬВОВИЧА СМОЛИНА : <СмолинПрЛор> (или <СмолинЛоренц>).

«ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА НА ОСНОВЕ ГИПЕРДВОЙНЫХ ЧИСЕЛ»

Читаю в аннотации:

Предлагаются преобразования, отличающиеся от лоренцевских преобразований отсутствием требования

y` = y, z` = z  в случае V_x = V; V_y = V_z = 0.­

Получены также общие преобразования для произвольного вектора V. Естественным языком данного подхода является язык гиперкомплексных чисел.

Обсуждаются некоторые следствия подобных преобразований в специальной теории относительности. Подчеркивается их связь с винтовым исчислением, с поляризационными и спиновыми свойствами движущихся с релятивистскими скоростями объектов. Приводится матричная формулировка этих преобразований.

Автор не ставил своей целью опровергнуть СТО, а только показывает, какие возможности открывают такие преобразования. Важная особенность подхода Смолина — он использовал не обычные кватернионы, а гиперкомплексные числа, основанные на двойных числах, то есть гипердвойные (напомню: двойные числа — один из видов комплексных чисел а + bе; в них а и b — действительные и  е² = +1); это естественно, ведь именно двойные числа связаны с псевдоевклидовой геометрией, играющей фундаментальную роль в СТО, и геометрией Лобачевского.

А теперь вспомним про наш новый вид преобразований (см. <Мемуар по относительности и единой теории поля>) с восстановленным в правах масштабным множителем, характеризующем эффект Доплера. При них как раз и не будет выполняться условие y` = y, z` = z, то есть происходит изменение масштабов в направлениях, перпендикулярных вектору скорости. Может быть, наши преобразования подводят физическую базу под формализм Смолина?

*  *  *

У этого автора имеются и другие публикации, например:

К солитонным решениям волновых уравнений в пространственном случае и гипердвойные числа. Препринт ИАЭ, М.:1985;

Гиперкомплексные преобразования Лоренца, эфир и остальная физика. — М. : Диалог-МГУ, 1999. — 105 с.

Нужна ли квантовая механика? — М. : МАКС Пресс, 2001. — 231 с.

Неклассическая электродинамика. Эфиродинамический подход на основе гиперкомплексных методов. — М. : МАКС Пресс, 2005. — 246 с.

 В 2011 г. вышла большая книга

«DNA REPLICATION. Current Advances»

Это сборник статей разных авторов, и одну из них написал исследователь из университетского Медицинского центра в Далласе You Cheng Xu:  <XuReplDNA>.

Называлась она

«Replication Demands an Amendment of the Double Helix»

В ней автор обратился к старой проблеме разделения двух нитей ДНК при репликации (и денатурации). Эту серьёзную трудность двойной спирали авторы модели осознавали — Ф. Крик подробно обсуждал её в статье «Строение вещества наследственности», опубликованной в октябрьском номере Scientific American за 1954 год. Она же стала причиной выдвижения альтернативных «бок о бок» моделей, о которых Крик писал в своей книге «What Mad Pursuit», вышедшей в 1988 г. (есть русский перевод).

You Cheng Xu приводит старые и новые данные, указывающие на то, что В ЦЕЛОМ две цепи молекулы НЕ ПЕРЕВИТЫ. Он придерживается такой версии: направление закрученности уотсон-криковской двойной спирали меняется вдоль цепи, то есть в ней чередуются правозакрученные и левозакрученные участки (the ambidextrous DNA model). Он пишет: «…the two strands in native DNA must bewound bi-directionally… ambidextrous DNA implies that the two strands are mainly winding right-handedly or left-handedly at the same time in a native DNA duplex, which is an amendment to the classical double helix model». Такое вот amendment.

В связи с этим хочу напомнить, что подобную идею выдвинул в 1981 г. Борис Саввич Филипп из Института прикладной физики АН МССР в Кишинёве. (Мы познакомились с ним на почве общего интереса к структуре ДНК на 1-ом Всесоюзном биофизическом съезде в Москве в августе 1982 г.) Затем этот взгляд поддерживали и другие авторы.

Ну а наш подход, как известно, другой: <Лента-спираль>.

 В 1991 г. у нас вышла автобиографическая книга «Время вспять, или Физик, физик, где ты был» (М. Наука) известного французского учёного Анатоля Абрагама (1914—2011). Он родился и десять лет прожил в Москве, прекрасно знал русскую литературу и сам перевёл на русский изданный в 1987-м оригинал под названием «De la physique avant toute chose» («Физика прежде всего», парафраз строки Верлена «музыка прежде всего»). А в 89-м появился и авторский перевод на английский — «Time Reversal, an autobiography».

Автор рассказывает о своём непростом пути, об увиденных изнутри разных сторонах научной жизни многих стран (Абрагам немало путешествовал; он был и крупным организатором науки — возглавлял физические исследования в Комиссариате по атомной энергии). Основная сфера его интересов — магнитный резонанс, ядерный магнетизм (читал курс по ним в Коллеж де Франс). Эта область во второй половине прошлого века интенсивно развивались, и Абрагам внёс в неё существенный вклад; награждён многими премиями, член нескольких академий.

Главное достоинство книги заключается в личности автора — это человек большой европейской культуры, настоящий интеллигент. Изложение ведётся в хорошем литературном стиле, в нём много «беззлобного остроумия» (слова Абрагама о Фрэнсисе Перрене), касающегося, в частности, известных людей, с которыми автору довелось встретиться в течение долгой жизни.

Я написал на книгу Абрагама рецензию «Возвращение утраченного времени», опубликованную в ХиЖ (1993, № 3): <АбрагамВремя>.