Как известно, в трёхмерном пространстве существуют ПЯТЬ правильных многогранников (Платоновых тел):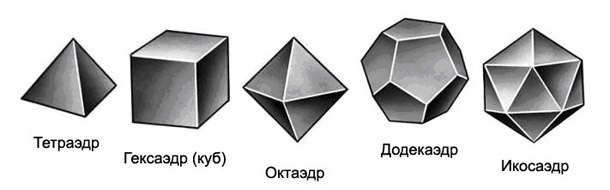

В четырёхмерном пространстве тоже существуют правильные политопы-многоячейники, причём, как открыл швейцарский математик Людвиг Шлефли в 1850-х годах, их там ШЕСТЬ.

В очень содержательной статье австралийского математика Джона Стиллвелла

«THE STORY OF THE 120-CELL» (Not. AMS, Jan. 2001) <Стилвел> 

в частности, показывается, что между некоторыми Платоновыми телами и их четырёхмерными «собратьями» (регулярными политопами) имеется очень простая связь: каждое вращение правильного 3D-многогранника задаётся единичным кватернионом (но нужно учесть, что два диаметрально противоположных кватерниона определяют одно и то же вращение, поэтому каждому вращению соответствует пара кватернионов), и все эти кватернионы, то есть четвёрки чисел, можно рассматривать как точки в 4D.

Тогда 24 точки, соответствующие 12 вращениям тетраэдра, служат вершинами правильного политопа в 4D, называемого 24-cell. Аналогично, 120 точек (удвоенная группа вращения икосаэдра) дают вершины самого сложного правильного политопа (600-cell). На рисунках показаны проекции (диаграммы Шлегеля) четырёхмерных двадцатичетырёхячейника и стодвадцатиячейника в трёхмерное пространство.

Но ведь между тетраэдром и икосаэдром есть ещё куб и октаэдр, имеющие одну и ту же группу вращения (то же верно для пары икосаэдр—додекаэдр). Она состоит из 24 элементов, и, значит, будет 48 кватернионов. Казалось бы, по аналогии, им тоже должен соответствовать правильный политоп в 4D, но среди давно установленных шести регулярных многоячейников такой не числится.

В статье Стиллвелла про этот политоп ничего не говорится. Видимо, не получился он регулярным («гадкий утёнок»), но всё равно он представляет большой интерес, потому что соответствует группе вращения куба. А она, как я думаю, играет ключевую роль в теории элементарных частиц: <Платоновы> (или <ПлатЭлЧаст>).

ДОПОЛНЕНИЕ (от 25.5.17)

Я вынес этот вопрос на математический сайт <МатемЖЖ>, и автор с ником eisenberg в посте от 24.5.17 сообщил о своих результатах рассмотрения данного политопа:

Строение такое: вершин 48, рёбер 7*48, граней 12*48, гиперграней же 6*48. Гиперграни все одинаковые, но неправильные. Грани тоже. А рёбра разные, двух разных длин. Длинные — это которые были рёбрами в 24-ке (её грани в общей выпуклой оболочке не сохранились, а вот рёбра да). Короткие — это которые между вершинами из разных двадцатьчетвёрок. В каждой грани и гиперграни коротких рёбер больше, чем длинных. А во всей фигуре — меньше.

Почему я считаю этот политоп важным? Потому что он есть геометрический образ группы вращения куба, а это фундаментальная симметрическая группа S4.
Мне вот какая мысль пришла в голову: группы вращений тетраэдра и икосаэдра привели к правильным политопам в 4D, и это знакопеременные группы A4 и A5. То есть можно предположить, что знакопеременные группы дают правильные политопы, а симметрическая — нет. Если так, то проливается некий новый свет на эти группы.